Comments
Follow Comments Sorted by time
guest_
· 4 years ago
· FIRST
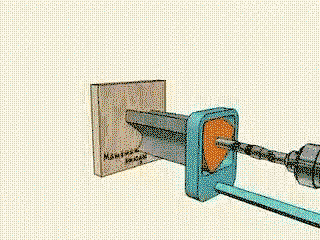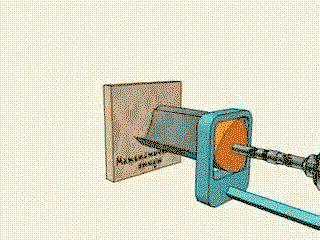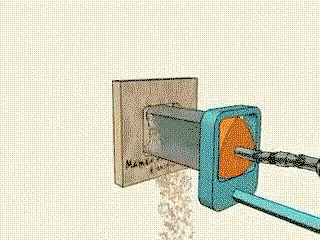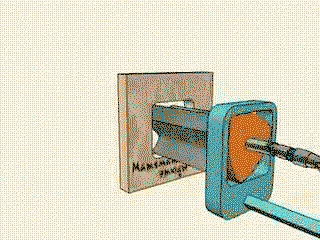
A three flanked hypotrochoid as pictured does not form a square. The trochoid geometry will not allow the leading edge to do so. The shape formed by this tool is commonly called a “squircle” “chamfered box” “rounded square” etc. it’s still a rather neat tool to watch and while seemingly simple, the math involved is quite impressive, at the least when we consider that at one point, fundamentals of geometry were undiscovered and someone came up with the idea, or found an application for the information. So very neat, but felt I would specify. Various Trochoids find their way into many neat designs from things like air conditioning compressors or other mechanical assemblies- right up to most rotary engine designs- most famously the Wankel/Mazda rotaries and derivatives.
xlaxxine
· 4 years ago
So basically it will form a square with rounded corners
2
cryoenthusiast
· 4 years ago
ok so why does it need a Reuleaux triangle to work. can't it also use a circle?
1
Show All
cryoenthusiast
· 4 years ago
i found an answer on the wiki for Reuleaux triangles
1
guest_
· 4 years ago
Sorry, I was asleep. I’m glad you found an answer though. For posterity, if anyone else is curious; and please feel free to share your answer if it differs from mine or has other information:
guest_
· 4 years ago
A working rotor is often shaped very close to a Reuleaux triangle, but is actually a curvilinear triangle. The sides are curved at a different angle. For those not aware- a realeaux triangle is formed by the intersection of 3 circles and has a constant width.
guest_
· 4 years ago
The path taken by the “rotor” of our epitrochoid will be influenced by several factors, but the distance from the center of the point of rotation to the working edge is a primary factor in the ultimate path that is traced, with any lobing or “cam” of the work shaft defining the path taken.
guest_
· 4 years ago
Because of this, the constant width of the Reuleaux triangle would ultimately follow a circles path. You’d have a circle rotating, off axis or not, in a circle. Our curvilinear triangle with its non constant width creates its own “cam” during on axis rotation. When you add a cam to the axis of rotation you now have 2 ellipsoid orbits and can create a vast array of of paths that would be impossible or impractical to do using purely circular paths.
cryoenthusiast
· 4 years ago
The answer i found, although my interpretation isn't as descriptive, was that reuleaux triangles are the shape that cover the most area when rotating inside a square, and that many rounded objects can spin inside and at least touch all four sides, the reuleaux triangle matches a square the best, not perfectly because it rounds off the corners. the device shown takes advantage of that by placing the cutting blades exactly on the corners of the rounded triangle and placing that inside the rounded square path it would take. as well as making it spin off center.
2
guest_
· 4 years ago
Pretty much the same answer it seems, but yours is more precise and concise. Let’s go with yours.
1